La Théorie Relative de la Monnaie fait remarquer qu’une conséquence directe de l’application d’un système relativiste, est la convergence dans le temps de la somme de la monnaie distribuée (ou émise – les deux termes étant dans ce paradigme parfaitement symétriques) envers chaque individu membre du système monétaire.
Comment cela est-il possible ?
Il faut considérer l’évolution de la somme de monnaie émise par chaque individu, quelle que soit sa situation initiale. Pour fixer les idées, imaginons donc pour une année A une masse monétaire partagée entre 3 individus : I1 possédant 100, I2 possédant 500 et I3 possédant 900. Soit une masse monétaire totale de 1500 (500 de moyenne monétaire par individu).
Pour l’année A I1 possède donc 6,7% de la monnaie I2 33,3% et I3 60%.
Le RdB relativiste est par exemple de 10%/an soit dans notre exemple 150 à partager entre les trois, soit 50 chacun. La nouvelle situation pour l’année (A+1) est donc que I1 possède 150, I2 aura 550 et I3 atteindra 950, pour une nouvelle masse monétaire de 1650.
Ce qui nous donne en proportion pour I1 : 150/1650 = 9,1% de la monnaie totale au lieu de 6,7% précédemment, pour I2 cela ne change pas : 550/1650 = 33,3%, et enfin pour I3 : 57,6% au lieu des 60% précédents.
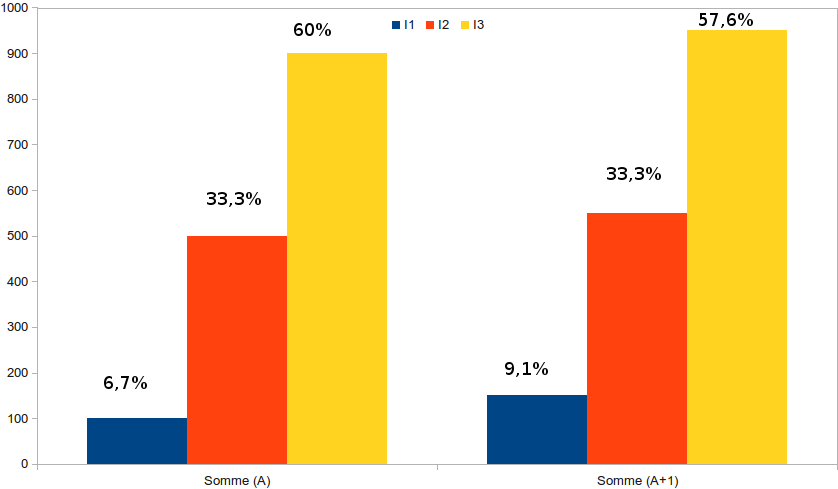
Et ceci vous l’aurez noté sans avoir recours à quelque taxe ou imposition que ce soit. Que la monnaie de I3 soit située dans un paradis fiscal ou pas, cela ne joue en rien sur le résultat.
Alors que se passe-t-il maintenant sur le long terme ? Eh bien, le calcul relativiste démontre que le taux assurant la symétrie temporelle pour une espérance de vie moyenne des individus de “ev” est très exactement c = ln(ev/2)/(ev/2). Cela signifie que le % de masse monétaire distribuée (ou émise) envers chaque individu, convergera vers un même % limite, au bout d’une 1/2 espérance de vie.
Regardons précisément cela sur un graphique, avec M(x) et M(y) représentant cette somme de monnaie individuellement émise relativement à deux individus X et Y, l’un partant de 50 de monnaie, l’autre partant de zéro (On peut considérer par exemple que X hérite et que Y n’hérite de rien, les deux étant nés en même temps), et faisant partie d’une communauté de 100 membres (la moyenne étant donc de 1% de la masse monétaire chacun).
Leur évolution converge, on le voit ici de deux façons, à la fois en terme quantitatif et bien sûr en terme relatif exprimé en % de la masse monétaire. On voit très clairement que leurs pouvoirs d’achat monétaires relatifs convergent de façon continue vers la moyenne de 1% (ils sont 100), ce qui est atteint avec un écart négligeable aux alentours de 40 ans, soit la demi-vie pour une espérance de vie de 80 ans.
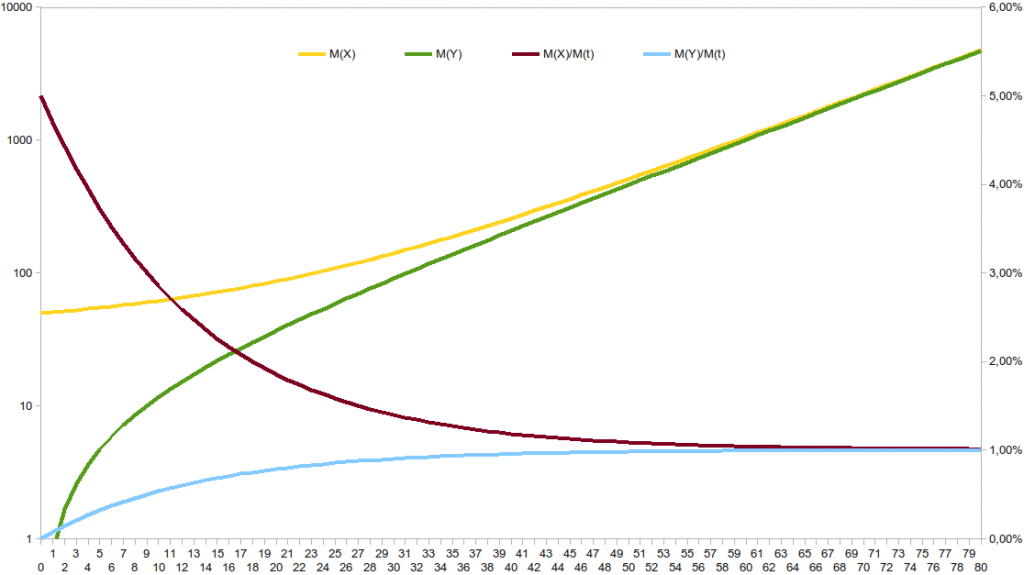
Et ce principe est intemporel. Il restera valable pour tout individu, qu’il naisse l’année A, l’année A+17, l’année A+137 ou n’importe quelle autre année.
Vous pouvez vous-même refaire ces calculs et réaliser des explications, en vous aidant au besoin du tableur LibreOffice téléchargeable en cliquant cette icône :
Ces résultats ne sont qu’une conséquence du paradigme de la TRM qui ne fait qu’appliquer des raisonnements cohérents avec ses fondements (Les 3 libertés économiques et le principe de relativité) pour établir ses théorèmes.
On notera en outre que la notion de “somme de la monnaie émise” n’est qu’une convention fondamentale pour l’explication, mais que si on change de référentiel en déclarant que les comptes sont affichés pour l’individu X comme Compte = M(x) – Masse Monétaire Moyenne, alors cette monnaie apparaît comme un crédit-débit individuel réparti entre tous, pouvant être négatif ou positif, toujours limité bien qu’en expansion.
Cette dernière remarque n’ayant pas plus d’intérêt fondamental que de déclarer qu’un objet se déplace à une vitesse de 100 km/h relativement à un observateur n°1 tandis qu’il se déplace à une vitesse nulle relativement à un observateur qui va lui-même à 100 km/h, aucun des deux n’ayant un point de vue absolu sur le phénomène observé.
La masse monétaire déclarée par la BCE en zone Euro, s’établit en 2013 aux alentours d’une moyenne de 35 000 € par citoyen (de 0 à 80 ans, soit 140 000 € pour une famille de 4).
