Après la valeur de c (dont la valeur numérique est une donnée empirique et non théorique) calculée selon d’autres méthodes originales et après la conférence donnée au Havre en Juin 2017, et surtout l’exposé de Mai 2018 aux RML11 de Douarnenez, qui donnait la voie à suivre (que personne n’a suivie !) on peut donner ici pour la première fois la méthode de calcul de c qui évacue le problème dimensionnel (la fonction logarithme s’applique à des nombres sans dimensions, sans quoi elle est sensible au choix de l’unité de mesure du temps choisie, un taux est donc correct, car s’agissant d’un rapport il est sans dimension) grâce à l’approche qui se fonde sur les données empiriques de l’espérance de vie mais aussi de son corollaire : le taux de mortalité.
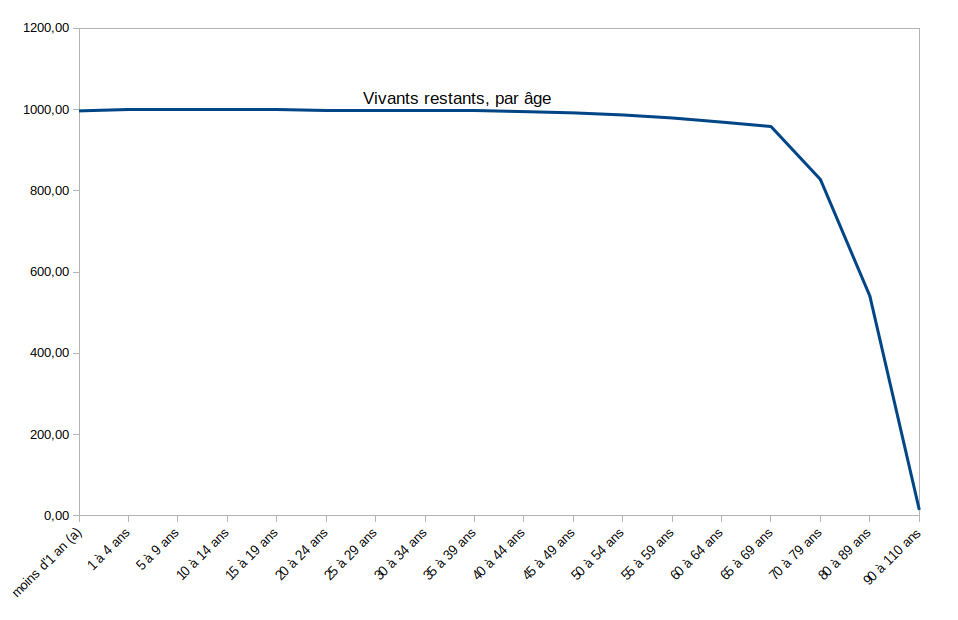
La taux de mortalité ainsi connu par âges (ici pour la France, en 2019), on vérifie par le calcul que pour la 1/2 vie de 40 ans, pour 1000 enfants nés, le cumul des décès par âges nous laisse un nombre de vivants restants après 39 ans de 996,76 / 1000. Et pour l’espérance de vie de 80 ans, il reste pour 1000 enfants nés un nombre de vivants de 827,98 / 1000, soit un taux de décès cumulé de 3,24 / 1000 (40 ans) et de 172,02 / 1000 (80 ans).
Le principe du calcul de « c » étant que la part de monnaie restante non-coproduite par les vivants, est de même ampleur que le cumul des décès de cette même génération.
Autrement dit, la moyenne n’étant jamais parfaitement atteinte par les vivants bien qu’ils s’en approchent au plus près, la part restante doit être de même ampleur que celle des décès cumulés au même point.
D’où l’on déduit, en nommant « x » le taux de mortalité cumulé à v/2 :
Dès lors, les valeurs de c empiriques correspondantes à ces deux points sont (pour la France en 2019, v = 80 ans, v/2 = 40 ans) :
Ce qui nous donne donc des valeurs de c autour de 14,33% / an tout à fait acceptables, et des valeurs de c proches et en deçà de 2,20% / an intenables (qui se soucie d’être monétisé au seuil du trépas ?).
